1. 기술통계
1.1 통계학의 종류
1) 기술 통계
- 데이터 분석 결과인 수치들을 활용하여 데이터 집합의 특성을 설명
(by.평균값, 분산, 표준편차, 범위, 히스토그램, 파이차트, 상자도표) - 기술통계는 통계량을 구하는 것 자체가 목적일 때가 많다.
2) 추론 통계
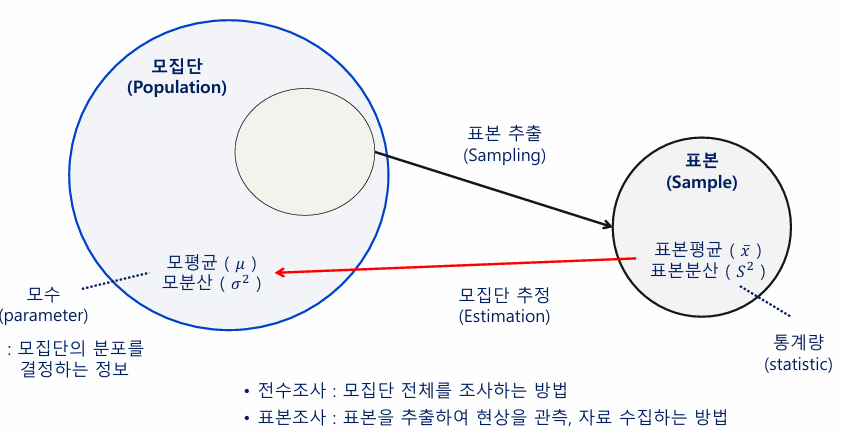
- 모집단에서 추출한 표본을 통해 모집단 의 특성을 표현
(LIKE 지방선거 출구조사, 제품 불량율 조사) - 따라서, 모집단이 더 중요한 통계
(모집단의 특성을 알 수 없을 때, 샘플로 모집단 특성 추론) - 추론
- 모수추정: 미지수인, 모집단의 모수에 대한 추측 또는 추측값을 정확도와 함께 제시
- 모수에 대한 가설검정: 모집단의 모수에 대한 여러 가설들이 적합한지 여부를 표본으로부터 판단함
1.2 표본의 추출 for 추론통계
- 확률적 표본 추출 (Probability sampling method)
: 동일한 확률 하에서 표본을 추출하는 방법- 무작위 표본 추출
: 모집단에서 표본을 기계적으로 추출하는 방법 - 체계적 표본 추출
: 모집단에서 특정한 규칙으로 표본을 추출하는 방법 - 층화 표본 추출
: 모집단을 특정 특성에 따라 여러 하위 집단으로 구분한 후, 집단의 규모에 비례하도록 추출하는 방법
- 무작위 표본 추출
- 비확률적 표본 추출 (Non-probability sampling method)
: 조사자가 자의로 표본을 추출하거나 조사 대상이 자발적으로 표본에 참여하는 방법.
표본 추출에 조사자나 참여자의 의사 반영
1.3 데이터의 중심경향성 측정 방법
** 중심경향성(Central Tendency)
: 표본 내의 원소들의 중심을 나타내는 지표. 평균, 중앙값, 최빈값 등으로 표현
- 평균(Mean)
: 연속적이고 정규 분포를 따르는 데이터에서 대표값을 구할 때 유용
사분위수 범위 Q2와 동일
- 장점: 데이터를 통합하여 하나의 대표값으로 표현
- 단점: 이상치(outliers)에 민감하여 극단적인 값에 영향을 받음
- 중앙값 (Median)
: 비대칭적이거나 이상치가 있을 때 사용- 장점: 이상치의 영향을 덜 받음
- 단점: 표본의 크기가 클 경우 정렬에 많은 시간 소요
- 최빈값 (Mode)
: 범주형 데이터에서 빈도가 가장 높은 값을 찾을 때 유용- 장점: 표본의 원소들의 빈도 분포를 잘 나타냄
- 단점: 표본 내에 최빈값이 존재하지 않을 수 있으며, 복수 개의 최빈값이 있을 수도 있음
- 가중평균 (Weighted Mean)
: 표본의 원소들의 값에 가중치를 부여하여 계산한 평균
모든 원소들의 값이 동일한 중요도를 가지지 않을 때 사용
- 예시
{1, 2, 3}와 각각의 가중치 {0.1, 0.3, 0.6}이 있을 때 가중평균은 (1*0.1 + 2*0.3 + 3*0.6) / (0.1 + 0.3 + 0.6)
5천원짜리 상품 8개와 9천원짜리 상품 2개를 구입했을 때 평균 구매값은 (5000 * 8 + 9000 * 2) / (8 + 2)
- 예시
- 조화평균 (Harmonic Mean)
: 역수 합의 평균의 역수
역수들이 산술평균을 이룰 때 사용한다(분자가 같고 분모가 다른 두 변수 a와 b)
평균을 구하려는 값에 전체 단위 중 분모가 변수로 작용할 경우. 즉, 변화율의 평균(평균 변화율)을 구할 때 사용
(평균속력(km/h)를 구할 때, 이동거리 뿐 아니라 같은 거리를 이동할 때 걸리는 시간도 변수이다)
- 예시
: 왕복 60km를 달린 왕 10km/h와 복 30km/h로 달렸을 때 평균속력를 구하는 경우, 전체 거리 60km는 고정되어 있으나 오가는 데 걸린 시간은 변화하는 값이 된다. 역수의 변화를 고려해여 평균적인 변화률을 구하기 위한 평균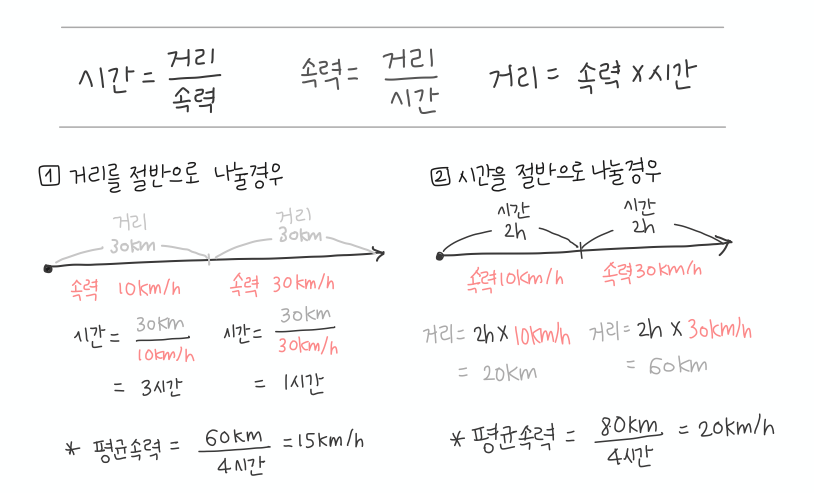
하단링크 참고: 1/n이 평균의 전부가 아니다,
- 예시
1.4 데이터의 산포의 측정
1) 분산과 표준편차
- 분산 (Variance)
: 데이터들이 평균에서 떨어져 분포되어 있는 정도(산포되어 있는 정도)- 각 데이터 값에서 평균을 뺀 값을 제곱한 후, 이 값들의 평균을 구함(편차의 제곱의 평균)
- 전체 데이터의 성질을 설명하는 평균이 갖는 정보값을 보충설명해준다.
- 평균이 1이나 분산이 클 경우, 이상치가 매우 높고, 평균의 설명력이 떨어지는 것
- 표준편차(Standard Deviation)
: 분산의 제곱근으로, 데이터가 평균에서 얼마나 떨어져 있는지에 대한 표준적인 거리를 나타냄
🔍 About 분산과 표준편차
편차의 제곱을 구하면 편차가 1보다 클 경우 실제보다 그 값이 증폭되고 1보다 작을 경우 실제보다 축소된다
데이터의 산포를 확인할 때, 데이터가 평균에서 떨어진 정도를 알기 위하여 편차의 크기를 파악하는 것이 중요하나 양수인지 음수인지는 중요하지 않다.
때문에 편차의 합이 0이 되는 문제를 해결하기 위하여, 음의 부호를 파악하는 방법이
1) 절댓값 2) 제곱
절댓값은 기호 사용의 불편합, 식 계산 및 변형의 어려움으로 인해, 식 자체가 갖는 성질 파악이 어려워 제곱을 사용한 편차 제곱의 평균, 즉 분산을 구한다.
그러나 분산은 그대로 사용하기에 너무 크다.
때문에, 기존 변량의 단위와 산포도 분산의 단위를 비슷하게 하기 위하여 표준편차의 개념을 추가한다. 제곱하여 구한 분산을 제곱근으로 되돌려 그 크기를 복구해준다. (표준편차와 평균은 단위를 나타내나, 분산은 단위를 나타내지 않는 것도 같은 이유)
2) 왜도와 첨도
통계에서 데이터 분포의 특성을 설명하는 지표
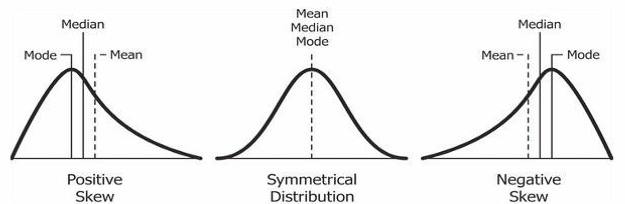
- 왜도(Skewness) : 분포의 비대칭성을 측정하는 지표
- 양의 왜도(Positive Skewness)
: 분포의 꼬리가 양수쪽으로
평균이 중앙값보다 큼 (예: 급여, 주택 가격 등) - 음의 왜도(Negative Skewness)
: 분포의 꼬리가 음수쪽으로
평균이 중앙값보다 작음 (예: 시험 점수 등)
- 양의 왜도(Positive Skewness)
- 첨도 (Kurtosis)
: 분포의 뾰족함과 꼬리의 두꺼움을 측정하는 지표
정규분포를 기준으로 높으면 양첨도, 낮으면 음첨도 (Kurtosis 3이 정규분포 첨도 기준 )- 양의 첨도 (Leptokurtic)
: 정규 분포보다 뾰족하고 꼬리가 두꺼운 분포(Kurtosis > 3)
극단적인 값(이상치)이 더 자주 발생함 - 음의 첨도 (Platykurtic)
: 정규 분포보다 평평하고 꼬리가 얇은 분포 (Kurtosis < 3)
극단적인 값이 덜 발생
- 양의 첨도 (Leptokurtic)
3) 사분위수 범위(Interquartile Range, IQR)
: 데이터의 중앙 50%가 포함된 범위로, Q3(3사분위수)와 Q1(1사분위수)의 차이
- 장점: 극단값의 영향을 덜 받음
1.5 확률 개념과 용어

- 표본공간(Sample Space)
: 실험을 통해 나타날 수 있는 모든 결과들의 집합 (가능성이 있는 모든 값의 집합) - 사건(Event)
: 표본공간의 부분집합 (표본점의 집합) - 표본점(Sample point)
: 모집단에서 무작위로 뽑은 하나의 표본 (단일 시행으로 얻은 표본)- 확률표본(Random sample)
: 모든 표본점(sample point)들이 동일한 확률로 추출된다는 조건 하에서 추출된 표본. 무작위 추출에서 얻은 표본
- 확률표본(Random sample)
- 확률변수(Random Variable)
: 일정한 확률로 일어나는 사건에 수치가 부여된 변수(실수값)
이산 확률변수와 연속 확률변수로 구분- 이산형 확률변수 (Discrete random variable)
: 확률 변수가 취할 수 있는 값이 유한하거나 셀 수 있는 경우- 확률질량함수(Probability Mass Function): 이산형 확률변수의 확률함수
- 이산형 확률변수에 의한 확률 분포: 이항분포, 기하분포, 포아송분포 등
- 연속형 확률변수 (Continuous random variable)
: 확률 변수가 취할 수 있는 값이 연속적인 경우. 가능한 값이 실수의 어느 특정 구간 전체에 해당
- 이산형 확률변수 (Discrete random variable)
- 확률
: 특정 사건이 일어날 가능성(수치로 사건이 발생할 가능성을 표현). 확률변수가 가진 확률. 0에서 1 사이의 값을 가짐 - 확률 함수(Probability Function)
: 사건이 발생할 확률을 함수로 나타낸 것 - 확률분포
: 확률 변수가 가질 수 있는 값들과 그 값들이 발생할 확률(들의 누적)을 나타내는 함수- 확률질량함수(Probability Mass Function): 이산형 확률변수의 확률함수
이산형 확률변수에 의한 확률 분포: 이항분포, 기하분포, 포아송분포 등 - 확률밀도함수(Probability Density Function) : 연속형 확률변수의 확률함수
연속형 확률변수에 의한 확률 분포 : 정규분포, 균일분포, t-분포, 카이제곱분포 등
- 확률질량함수(Probability Mass Function): 이산형 확률변수의 확률함수
🔍확률변수-확률함수-확률분포-PMF/PDF
표본공간에서 일어나는 사건의 확률변수들은 확률을 갖고
(변수는 이산형이기도, 연속형이기도 하다),
확률변수가 갖는 확률들은 확률 함수로 나타난다
(이산형이면 PMF, 연속형이면 PDF를 갖는다).
확률함수들로 확률 분포를 그리면(subset),
확률 분포는 다시 확률질량함수로 함수화되어 표현된다.
확률분포: (x: 사건 > 확률 변수) + (y: 확률 > 확률함수)
1.6 확률분포
1.6.1 이산 확률 분포
1) 베르누이 분포
: 두 가지 결과(성공 또는 실패)가 있는 단일 시행의 확률분포
- 베르누이의 기댓값은 1회 시행에 대한 확률(p)이다(정의에 따라, 단일 시행의 확률분포이므로).
- 확률변수 𝑋 : 성공일때 1, 실패일때 0의 값
2) 이항분포
: 베르누이 시행을 다회 시행 시 성공이 나오는 횟수의 분포
- n 회 시행에서 성공의 가능성 분포(sigma np=1)
- 확률변수 𝑋 : 𝑛번의 독립적인 시행 중 성공 횟수
3) 푸아송 분포
: 단위 시간(또는 단위 공간)에서 특정 사건의 발생 빈도를 나타내는 분포
- 사건의 빈도를 모델링할 경우 사용
- 확률변수 𝑋 : 일정한 시간에서 발생하는 사건의 횟수
- 예) 일정 시간동안 입질이 올 횟수의 분포
2.6.2 연속 확률 분포
1) 정규 분포 (Normal Distribution)(=가우시안분포)
: 평균 𝜇를 중심으로 대칭
- 확률변수의 68%가 𝜇±𝜎, 95%가 𝜇±2𝜎, 99.7%가 𝜇±3𝜎 범위 내에 위치함
- 표준정규분포
: 평균이 0, 표준편차가 1인 정규분포
2) 지수 분포 (Exponential Distribution)
: 사건 간의 시간 간격에 대한 분포
- 주로 포아송 과정에서 시간 간격을 모델링하는 데 사용
- 예) 콜센터 대기 시간 : 다음 전화가 걸려올 때까지의 시간
3) 카이제곱 분포
: 정규 분포를 따르는 독립적인 변수들의 제곱의 합의 분포로, 모집단의 분산을 추정할 때 주로 사용
- 적합도 검정과 분산분석에 사용
- 적합도 검정: 관찰 데이터가 기대 분포와 일치하는지 검정
- 분산 분석: 여러 집단 분산을 비교
2. 추론통계
2.1 추론
: 추론통계는 모집단에 대한 정보를 찾는 것.
따라서 추론은 모수 추정과 모수에 대한 가설검정이며, 2가지 종류가 있다.
1) 추정: 미지수인, 모집단의 모수에 대한 추측 또는 추측값을 정확도와 함께 제시
- 점추정
- 정의 : 모집단의 모수를 단일 값(점)으로 추정하는 방법
- 대푯값으로는 표본평균, 표본분산 등이 사용됨
- 구간추정 (Interval Estimation)
- 정의 : 모집단의 모수를 포함할 것으로 예상되는 구간을 제시하는 방법
- 신뢰구간과 신뢰수준으로 구성되며, 유의수준으로 신뢰수준을, 신뢰 수준으로 신뢰 구간 설정
- 예) 유의수준 5%로, 신뢰수준 95%인 신뢰구간을 설정한다.
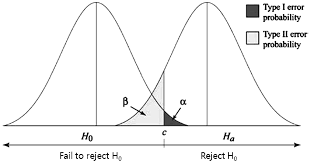
- 유의수준 𝛼 : 모수가 신뢰구간에 포함되지 않을 확률
- 신뢰수준 : 모수가 해당 구간에 포함될 확률; 𝑃(𝑎 ≤𝜇≤𝑏) =1− 𝛼
- 신뢰구간 : 모수가 포함될 것으로 예상되는 범위
- 오른쪽이 대립가설 왼쪽이 귀무가설상 분포라고 보면, 귀무가설이 참이라는 가정 하에 엄청 극단적인 (유의수준 5%) 값이 표본에서 지속적으로 관측된다면 귀무가설이 거짓이라고 보는 것이다.
- 정의 : 모집단의 모수를 포함할 것으로 예상되는 구간을 제시하는 방법
2) 가설검정
: 어떤 추측이나 주장, 가설에 대해 타당성을 조사하는 작업(가설이 맞다 그르다)
가설추정은 옳다, 그르다의 가정이기 때문에 쉽게 독립성 검증의 수단으로도 이어진다 (맞다/틀리다 > 같다/다르다).
- 가설검정 단계:
가설 수립 > 유의수준 설정 > 검정 통계량 계산 (t-검정; 독립성 검정) > 기각/채택 결정 (P-value; 진짜 믿을만한가?) - 🔍 귀무가설 vs 대립가설
귀무가설: 티니핑들은 똑같이 생겼다.
대립가설: 티니핑들은 다르게 생겼다.
귀무가설은 전통적이고 통념에 가까운 지식(정보, 가설)입니다.
그래서 이 가설을 부정하려면(모두가 인정해야 함),
'귀무가설이 일반적이지 않았네?!' 라고 증명해주어야해요.
귀무가설을 기각하고 대립가설이 더 진짜에 가깝다고(더 잦다고) 설득하는 것입니다.
대립가설은 귀무가설이 기각되었을 때 당연히 따라오는 결과여야 하므로,
귀무가설과 대립가설은 yes or no 이분법적입니다
(티니핑 생긴게 다 똑같지;기각 > 아니야 달라;채택).
+) 실험할 때는 '유의미하게 같다, 다르다 '등의 가설이 많이 사용됩니다.
- P-value
: 귀무가설 하에 있는 관측된 데이터가 발생할 확률.
귀무가설 관측 확률, 귀무가설이 참일 확률 (H0을 지지하는 값)- P-value가 유의수준 0.05보다 작으면 귀무가설 기각 (효과 있다)
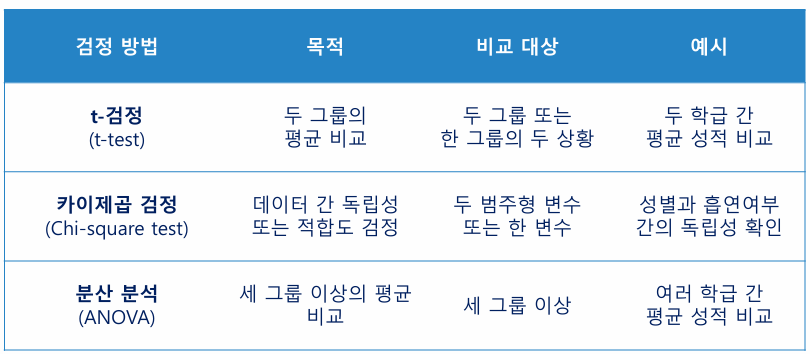
3) 가설검정 방법
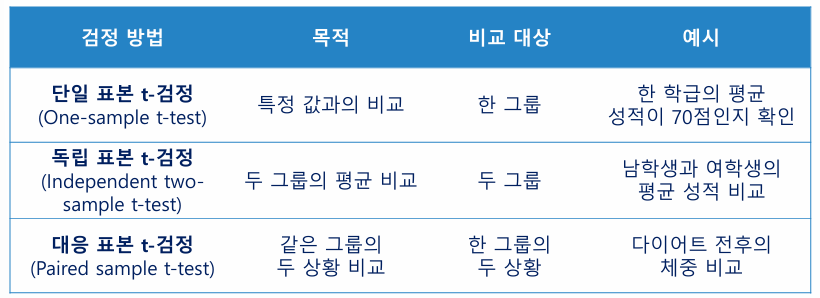
- t-검정(t-test)
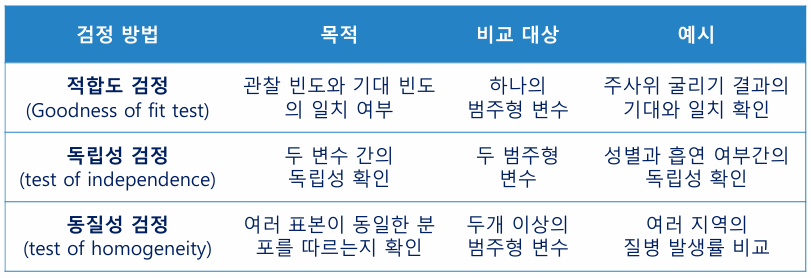
: 2 그룹 간의 평균의 차이가 유의미한지 확인하고자 할 때 주로 사용 - 카이제곱 검정(Chi-square test)
: 범주형 데이터에서 기대 빈도와 관찰된 빈도 간의 차이를 확인할 때 사용
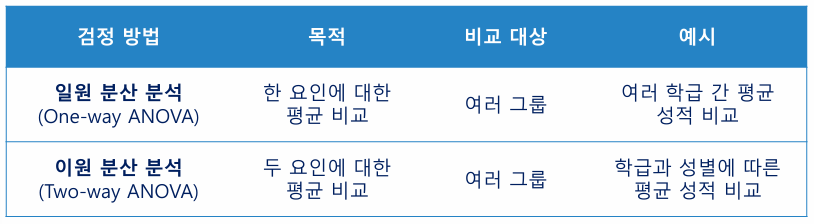
두 범주형 데이터에서 변수 간 독립성 여부를 검정할 때 사용 - 분산 분석(ANOVA : Analysis Of VAriance)
: 3개 이상의 집단에 대한 평균 차이를 검증하는 분석 방법
2.2 오류
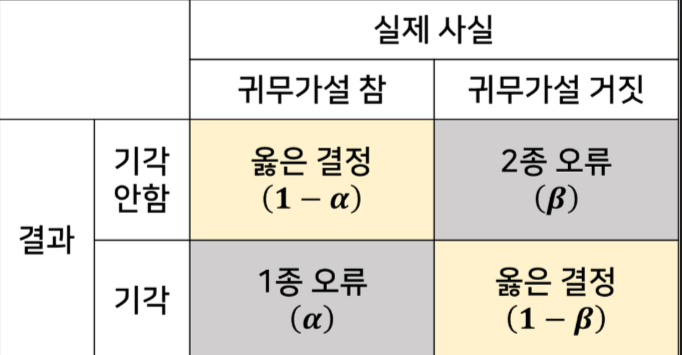
- 1종 오류 (Type I Error) : 귀무가설이 참인데도 불구하고 이를 기각하는 오류 (FN)
- 2종 오류 (Type II Error) : 대립가설이 참인데도 불구하고 귀무가설을 기각하지 않는 오류 (FP)
2.3 가설검정 및 ML 성능평가 지표
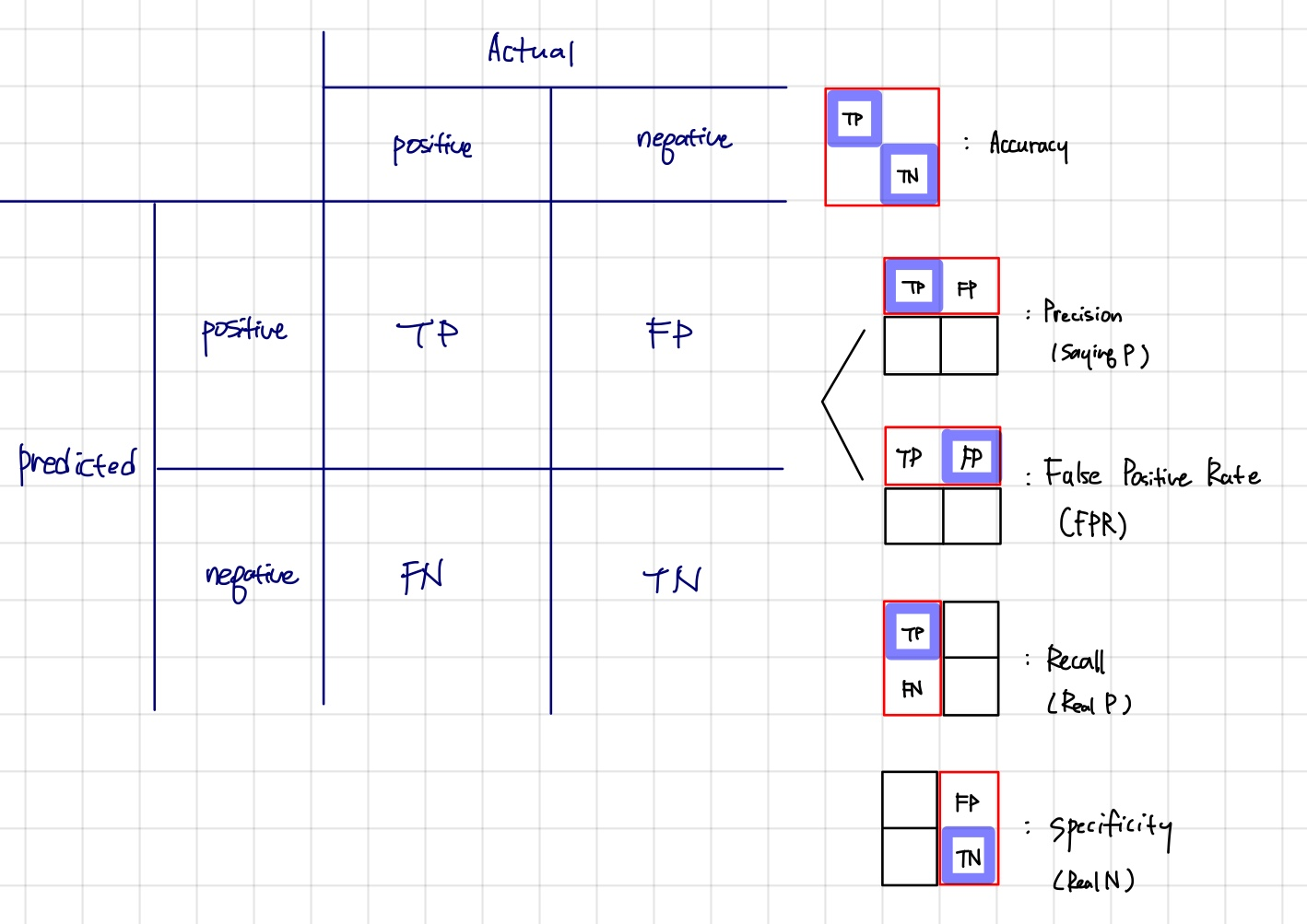

- 정밀도(accuracy)
: True/All
TP+TN/TP+FN+FP+TN - 정밀도(precision)
: TP/saying P
TP/TP+FP
True 검출 성능
실제 음성 데이터를 양성으로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우
ex) 스팸메일 잘 구분하는가? - 재현율(recall)
: TP/Real P
TP/TP+FN
실제 양성 데이터를 음성 데이터로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우
Positive 검출 성능
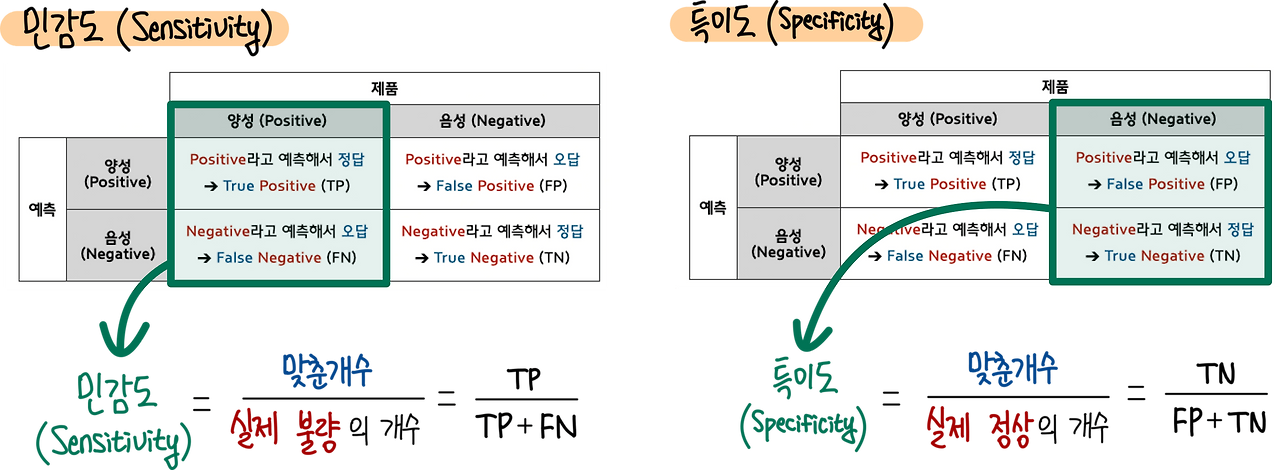
ex) 암환자를 놓치지 않았는가? - 특이도(specificity)
: TN/Real N
TN/TN+FP
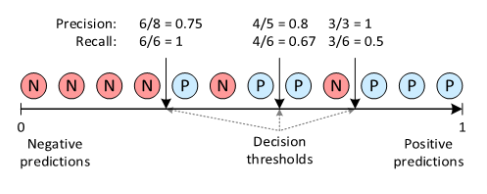
🔍 Precision과 Recall의 관계
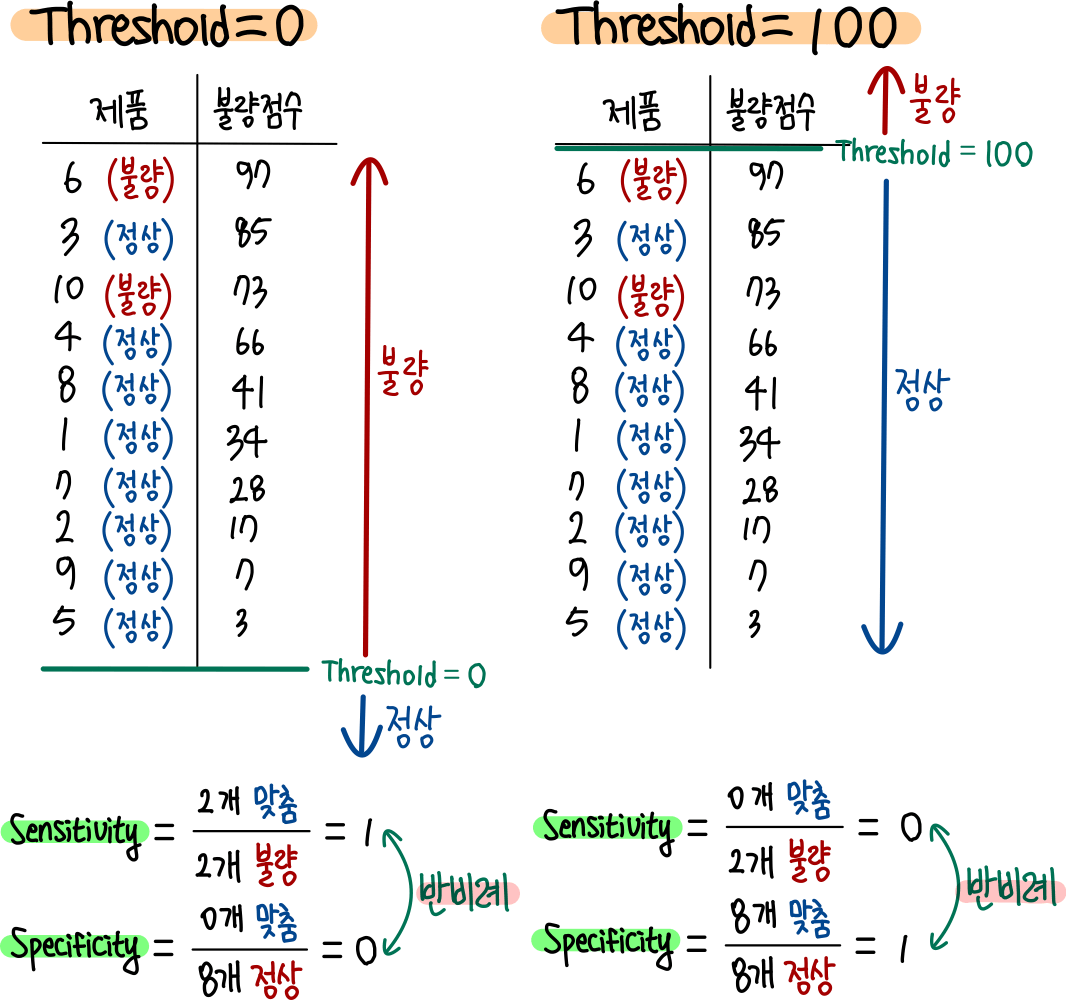
Precision과 Recall은 trade-off 관계있다.
임계값을 올리면(max), positive 기준이 높아지면서 precision이 상승하는 반면,
모든 샘플을 negative로 판단한다는 것이기도 하므로, FN이 증가하면서 recall이 감소한다.
precision = positves over threshold /every samples over threshold(감소)
recall = positves over threshold /positives in every sample(고정)
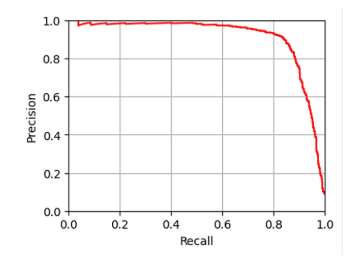
🔍 Recall과 Specificity의 관계
서로 반비례 관계
3. 상관분석
: 두 변수의 관계를 정량적으로 평가하는 통계 기법으로, 한 변수가 변함에 따라 다른 변수가 어떻게 변화하는지 파악 가능
- 상관계수 (Correlation Coefficient)
: 두 변수 간의 관계의 강도와 방향을 나타내는 수치 - 상관관계의 강도
: 상관계수의 절대값을 기준으로, 약한 상관관계 (~0.3), 중간 상관관계 (0.3~0.7), 강한 상관관계(0.7~)
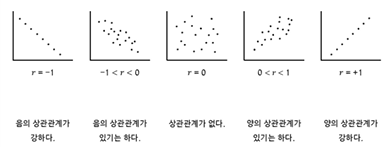
상관성은 X의 증감이 Y의 증감에 미치는 영향을 정량화한것인데, 우연의 일치로 높게 나올 수 있다
인과가 있으면 상관이 잇는데, 상관이 있다고 인과가 있지는 않는 것. 상관이 높아도 직접 인과(영향)은 알 수 없음
ex) 아이스크림 판매량과 해변 사고률
1) 피어슨 상관계수 (Pearson Correlation Coefficient, 𝑟)
- 측정 대상
: 가장 널리 사용되는 상관계수. 변수간의 선형관계를 측정하며, 데이터가 정규분포를 따르고 연속적인 경우 적합 - 장점 : 데이터의 선형 관계를 직접적으로 반영하며, 해석이 직관적
- 단점 : 두 변수 간의 관계가 비선형 관계일 경우 이를 제대로 반영하지 못함
- 예시: 키와 몸무게 간의 관계 (일반적으로 키가 큰 사람이 몸무게도 더 나가는 경향이 있을 때 사용)
- 계산 방법
: 두 변수의 공분산을 각 변수의 표준편차로 나누어 계산. 즉, 두 변수가 함께 변하는 정도를 표준편차로 정규화한 값
(잘 보면 공분산은 (X-Xbar)^2이 (X-Xbar)(Y-Ybar)로 치환된 것이 공분산임을 알 수 있다)
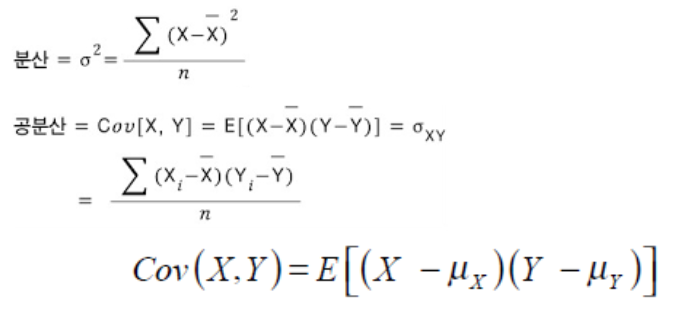
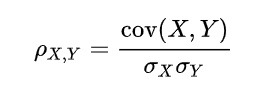
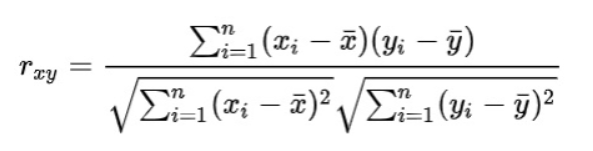
- 유의성 검정
: 계수가 정말 유의미한지 검정이 필요하다. 정말 두 변수간의 유의성이 있는가?
- 피어슨 상관계수의 유의성 검정을 위해, 다시말해 변수 간 독립성을 검정하기 위해 '피어슨 상관계수가 0이다'를 H0로 두고 검정한다.
- 이 때, t-검정을 이용하며 검정통계량 t는 피어슨 상관계수를 이용해 계산한다.
- t값의 절대값이 클 수록 상관계수가 통계적으로 유의미하다.
- 정리하자면, 피어슨 상관계수(가 정말 참인가)에 대한 검정은 분포를 가정하는 모수적검정이다.
🔍 python function
#1 function
df.corr(method='pearson')
#2 scipy
from scipy.stats import pearsonr
correlation_coefficient, p_value = pearsonr(df['colA'], df['colB'])
2) 스피어만 상관계수 (Spearman's Rank Correlation Coefficient, 𝑟𝑠 )
- 측정 대상
: 순위형이거나 비선형 변수 간 관계 측정- 순위기반 상관관계로, 순위 차이에 따라 값을 계산하기 때문에 변수 간의 비선형 관계 반영 가능
- 피어슨 상관관계 분석은 데이터가 정규성을 가정하므로, 아웃라이어들이 많거나 정규성을 따르지 않는 데이터들이 있을 때 상관계수가 그 영향을 받아 데이터 특성을 잘 반영하지 못한다. 이런 경우 스피어만 상관계수를 사용하면 좋다. 스피어만 상관계수는 아웃라이어를 고려하기 위하여, 순위 데이터로 변수값을 변환한 후 상관계수를 계산하기 때문이다.
- 장점 : 비선형 관계와 이상치에 민감하지 않음
- 단점 : 데이터의 순위 정보만 사용하여 정보 손실이 발생할 수 있음 (원래 데이터의 크기 정보 등)
- 해석: 𝑟𝑠 가 0일 때, 두 변수가 통계적으로 서로 독립
- 예시: 학생 성적 순위와 스포츠 성적 순위 간의 관계
(학생들의 성적과 스포트 성적 간의 관계 분석 시 점수를 순위로 변경하여 상관관계 분석) - 계산 방법 : 각 변수의 순위를 매긴 후, 그 순위들 간의 상관계수를 계산한다. 하단 이미지 좌측 식의 d는 순위차이고, d가 작을 수록 스피어만 순위 상관계수는 증가하며, 이는 X와 Y의 크기 변화가 함께 일어나는 것
- 각 변수의 값들을 그들의 순위로 변환합니다.
- 각 관측치 쌍에 대해 순위 차이를 계산합니다.
- 순위 차이를 제곱하고, 이 제곱값들의 합을 구합니다.
- 다음 공식을 사용하여 스피어만 상관계수를 계산합니다:
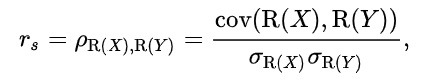

- 유의성 검정
: '스피어만 상관계수는 0'이 귀무가설로 검정
🔍 python function
from scipy.stats import pearsonr, spearmanr
spearmanr(df['colA'], df['colB'])
3) 켄달의 타우 (Kendall's Tau, Kendall's Rank Correlation Coefficient, 𝜏)
- 측정 대상
: 순위 관계를 고려한, 변수 순서 간의 상관성을 측정(작은 데이터셋에 적합)
스피어만보다 범위를 좁힌 것이 켄달의 타우
(Spearman 상관 계수보다 더 보수적인 해석을 제공하며, 순위가 동등한 데이터가 많을 때 주로 사용) - 해석 : 피어슨 상관계수와 동일하게 해석함. 켄달의 타우가 0일 때, 두 변수가 통계적으로 서로 독립
- 장점 : 순위 정보에 기반하여 비선형 관계도 잘 반영
- 단점 : 계산이 복잡하며, 해석이 어려울 수 있음 (특히 데이터셋이 클 경우 계산 부담 증가)
- 예시 : 직무 수행 순위와 승진 순위 간의 관계
- 계산방법 : 순위 쌍 간의 일치와 불일치를 비교하여 상관관계를 계산
𝜏 = C-D / C+D - C: 일치하는 순서쌍(concordant pairs)의 개수. 즉, 두 변수의 순서가 동일한 순서쌍
- D: 불일치하는 순서쌍(discordant pairs)의 개수. 즉, 두 변수의 순서가 반대인 순서쌍
- 유의성 검정
: 두 변수가 서로 독립인지 검정하기 위해 H0 '켄달의 타우가 0이다'를 검정
🔍 python funcion
from scipy.stats import kendalltau
kendall_corr, kendall_p = kendalltau(df['X'], df['Y'])
4. 데이터 시각화
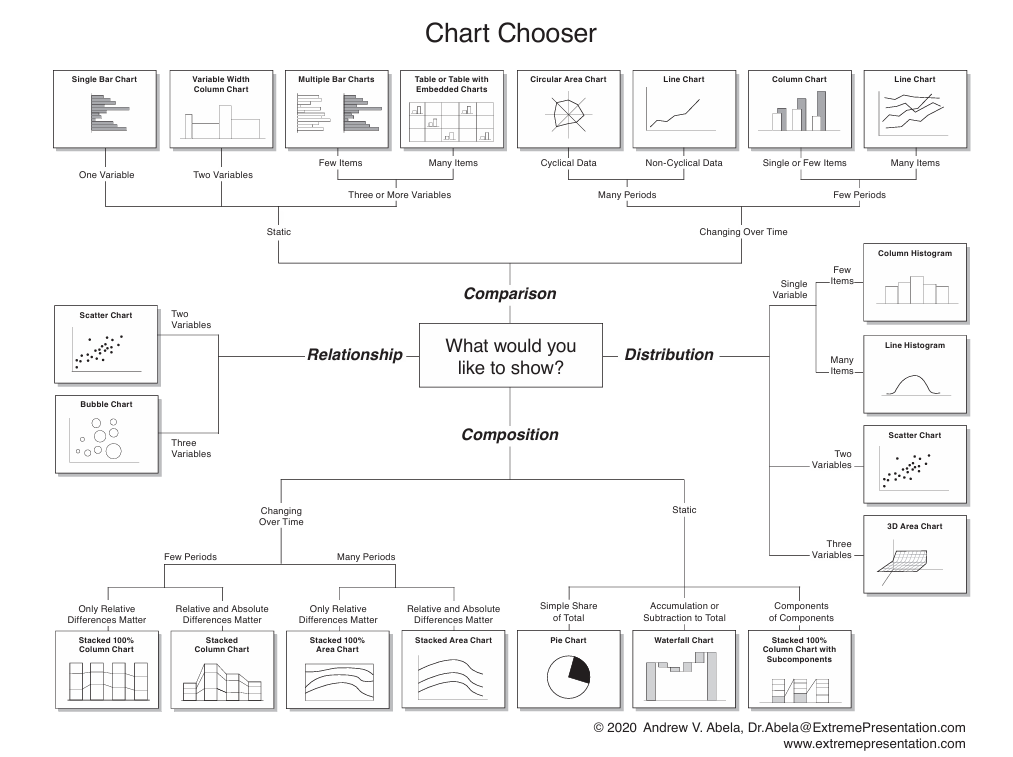
1) 막대 차트(Bar Chart)
- 아이템, 카테고리 등을 비교
2) 선 차트(Line Chart)
- 선으로 표현되는 연속된 점들 간에 의미 있는 관계일 때, 시간 경과에 따른 추세 표현에 주로 사용
- 다른 차트의 가독성을 침해하지 않기 때문에 섞어쓰기 좋다(ex. 막대그래프와 혼합)
3) 영역차트
- 면적에 의미 부여해 시간에 따른 변화의 크기를 시각화
4) 히스토그램
- 막대그래프 + 전체 분포 표현
- 분포 현황 파악(연속적인 값을 나열하여 비교) 및 데이터의 대칭성을 확인
데이터의 수가 많거나, 각 데이터의 비율이 균등할 경우 시각화 효과가 떨어짐
5) 파이차트
- 전체에 대한 비율
6) 도넛차트
- 파이차트와 형태적 유사성을 갖고 있으나, 분포를 파악하기 유리(막대그래프와 성질 유사-펼치면 형태도 동일)
7) 게이지 차트
- 한 항목에 대한 정보를 강력히 표현(대시보드와 강한 연관성)
- 목표의 달성 정도를 파악하기 위해 사용되는 시각화 방법
8) 버블차트
- 색, 좌푯값(x,y)과 함께 데이터의 크기(z)를 표시하여 시각화 하는 방법
- 분석 대상의 크기의 시각적 표현 또는 잠재적 가치의 표현에 주로 사용됨
- 데이터의 정확한 크기(z)를 비교하기에는 적합하지 않음
9) 트리맵
- 자식차트 총합 = 부모차트 면적(전체와 부분의 비율로 양을 파악)
- 계층적 데이터를 표시하는 데이터 시각화
- 기술 트리의 노드들을 중첩된 사각형의 집합으로 표현하여 패턴 식별 및 신속한 비교를 도와줌
참고문헌
[분산과 표준편차] 분산은 왜 제곱을 하는가? : 네이버 블로그
상관분석, 상관계수 (Correlation Coefficient) : 네이버 블로그
피어슨 상관계수, 스피어만 상관계수, 켄달의 타우 완벽비교
1/n이 평균의 전부가 아니다, 산술평균+기하평균+조화평균의 공식과 예시
소고
다시 수학을 배우니까 재밌다.
성적에 쫓기지 않아도 되고 내가 정말 못하는 문제풀이 없이 이론만 배우니까 일견 퍼즐같다.
그리고 나는 수학 문제를 풀때 그래서 이게 뭔 쓸모가 있는 거지? 무의식중에 의문이 생겼는데,
추후 사용될것이 확실하니 더 적극적이 된다
규칙을 찾는 것이 재밌다.
의외의 존재는 당황스럽지만 흥미롭다.
매력적인 오류를 찾는 것과 의외를 만드는 것이 크게 다를까?
'공부 > ML & AI' 카테고리의 다른 글
| ML 모델과 알고리즘 기본 (5): 회귀모델 평가지표 (0) | 2025.01.29 |
|---|---|
| ML 모델과 알고리즘 기본 (4): 회귀모델 (0) | 2025.01.29 |
| ML 모델과 알고리즘 기본 (3) : 분류모델 평가지표 (0) | 2025.01.28 |
| ML 모델과 알고리즘 기본 (2) : 분류모델 (0) | 2025.01.27 |
| 생성 AI 이론 및 실습 (0) | 2025.01.14 |



